වෘත්ත
පළමුවෙන් වෘත්තයක අංගහදුනා ගනිමු.
centre = කේන්ද්රය
radius = අරය
diameter=විෂ්කම්භය
circumference=පරිදිය
ප්රමේයය -
වෘත්ත චාපයක් මගින් වෘත්තයේ කේන්ද්රය මත ආපාතනය කෙරෙන
කෝණය, එම චාපය මගින් වෘත්තයේ ඉතිරි කොටස මත ආපාතනය
කෙරෙන කෝණය මෙන් දෙගුණයක් වේ.
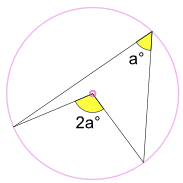

වෘත්තයක චාපයකින් කේන්ද්රය මත ආපාතනය කරන කෝණය එම චාපයේ ඉතිරි කොටස
මත ආපාතනය කරන කෝණය මෙන් දෙගුණයක් වේ, යන ප්රමේයයේ විධිමත් සාධනය......
සාධනය කළ යුත්ත:AOB ∢=2AOC∢බව
නිර්මාණය: COරේඛාව X දක්වා දික් කිරීම
සාධනය: OA=OC(එකම වෘත්තයේ අර)
OAC∢=OCA∢ (සමද්විපාද ත්රිකෝණයක සමාන
පාදවලට සම්මුඛ කෝණ සමාන නිසා)
OCA∢ + OAC∢=XOA∢ (ත්රිකෝණයක පාදයක් දික් කිරීමෙන්
සෑදෙන බාහිර කෝණය අභ්යන්තර
සම්මුඛ කෝණ දෙකේ එකතුවට සමාන නිසා)
ප්රමේයය -
වෘත්තයක එකම ඛණ්ඩයේ කෝණ සමාන වේ.





ප්රමේයය -
අර්ධ වෘත්තයේ කෝණ සෘජු කෝණයක් වේ.



ප්රමේයය -
පළමුවෙන් වෘත්තයක අංගහදුනා ගනිමු.
centre = කේන්ද්රය
radius = අරය
diameter=විෂ්කම්භය
circumference=පරිදිය
ප්රමේයය -
වෘත්ත චාපයක් මගින් වෘත්තයේ කේන්ද්රය මත ආපාතනය කෙරෙන
කෝණය, එම චාපය මගින් වෘත්තයේ ඉතිරි කොටස මත ආපාතනය
කෙරෙන කෝණය මෙන් දෙගුණයක් වේ.

වෘත්තයක චාපයකින් කේන්ද්රය මත ආපාතනය කරන කෝණය එම චාපයේ ඉතිරි කොටස
මත ආපාතනය කරන කෝණය මෙන් දෙගුණයක් වේ, යන ප්රමේයයේ විධිමත් සාධනය......
දත්තය: o කේන්ද්රය වූ වෘත්තය මත A,B සහ C ලක්ෂ්ය පිහිටා ඇත.
සාධනය කළ යුත්ත:AOB ∢=2AOC∢බව
නිර්මාණය: COරේඛාව X දක්වා දික් කිරීම
සාධනය: OA=OC(එකම වෘත්තයේ අර)
OAC∢=OCA∢ (සමද්විපාද ත්රිකෝණයක සමාන
පාදවලට සම්මුඛ කෝණ සමාන නිසා)
OCA∢ + OAC∢=XOA∢ (ත්රිකෝණයක පාදයක් දික් කිරීමෙන්
සෑදෙන බාහිර කෝණය අභ්යන්තර
සම්මුඛ කෝණ දෙකේ එකතුවට සමාන නිසා)
ප්රමේයය -
වෘත්තයක එකම ඛණ්ඩයේ කෝණ සමාන වේ.
ප්රමේයය -
අර්ධ වෘත්තයේ කෝණ සෘජු කෝණයක් වේ.
ප්රමේයය -



Good and usefull
ReplyDeleteYes ! Very usefull
ReplyDeleteUse this
ReplyDelete